La mise en correspondance d'images suppose le traitement d'une quantité énorme d'informations que l'on est tenté de réduire pour ne garder qu'une partie nécessaire à l'élaboration d'une méthode de fusion de deux images stéréo.

Cette simplification des images est basée sur des indices visuels [AYAC89] qui contiennent de manière concise des informations importantes pour le traitement des images.

Notre chaîne de traitement nécessite la détermination de points homologues suffisamment précis pour que l'on puisse s'appuyer sur ceux-ci afin de calculer la correspondance entre les deux images du couple stéréo. Cette relation entre les deux images est utilisée pour diminuer le calcul nécessaire à la fusion des images, en se basant sur un modèle géométrique épipolaire qui donne les contraintes géométriques entre les images issues des conditions de prise du vue. Ces contraintes facilitent les algorithmes de traitement d'image, limitent les calculs et permettent d'évaluer la fiabilité des résultats obtenus.

Différentes approches existent pour extraire des points homologues entre deux images, les principales sont de mettre en correspondance des régions d'images homologues (ou zones de l'image homogènes au sens d'un certain critère), ou de comparer les contours des objets (ou zones de transition entre régions homogènes) contenus dans les images.

C'est cette dernière approche que nous avons choisie car elle nous permet d'avoir des points homologues assez précis sur lesquels nous nous appuierons pour initialiser le processus de mise en correspondance des images. Le nombre de couples de points homologues nécessaires à l'étape suivante de notre chaîne de traitement étant limité, ceci ne nous oblige pas à chercher à extraire la totalité des contours, mais plutôt un ensemble d'éléments suffisamment caractéristiques pour apparier le nombre nécessaire de points.

La technique d'appariement s'appuie sur un critère de forme qui doit être suffisamment localisé pour obtenir une correspondance entre des pixels des deux images. Il est donc utile de coder les contours d'une manière qui permette d'obtenir cette précision d'appariement et de s'affranchir d'une part des problèmes de rotation d'une image par rapport à l'autre et dans une certaine mesure d'éventuelles variations de la taille des objets entre les deux images d'autre part.

Après une description des caractéristiques des contours, nous citerons les familles d'extracteurs de contours et nous décrirons le codage de Freeman [FREEMA] que nous avons choisi pour représenter les contours.

Les contours d'une image correspondent aux discontinuités de l'intensité lumineuse.

Dans les images optiques, cette intensité est fonction de trois paramètres:

- I:l'intensité lumineuse incidente

- n:le vecteur normal à l'élément de surface

- R:la réflectance de l'élément de surface.

Les contours correspondent à la discontinuité d'un ou de plusieurs de ces paramètres.

Les arêtes et les marques sont intrinsèques, c'est à dire invariantes ou presque par changement de point de vue, ce qui est une propriété importante en stéréovision. Les ombres sont intrinsèques si l'orientation de la source lumineuse par rapport à la scène ne change pas entre les prises de vue.

Les occultations dépendent du point de vue et peuvent poser des problèmes. Ils donnent lieu à des contours apparents, c'est à dire que l'on calcule des contours à partir d'ensembles de points qui ne sont pas les mêmes d'une image à l'autre (ex: image stéréo d'une sphère dans l'espace).

Les caractéristiques d'un contour sont:

- Robustesse au bruit: il faut éliminer les points qui du fait des imperfections du système de prise de vue présentent les caractéristiques d'un contour, afin d'obtenir un contour aussi proche que celui obtenu sans influence du bruit.

De nombreux auteurs se sont penchés sur le problème de l'extraction de contours.

Un point contour étant caractérisé par un fort gradient ou variation de l'intensité lumineuse, le premier opérateur de détection de contour qui fut développé par Robert est une application directe de la formule d'une dérivée. Il est formé de deux masques H1 et H2 donnant le gradient respectivement dans les directions PI/4 et 3PI/4 :

L'application de ces deux masques pour un point M(x,y) de l'image donne g1 et g2.

L'amplitude est donnée par

que l'on peut approximer par:

La direction du gradient est fonction de l'arc-tangente entre g1 et g2

Cet opérateur est très localisé, et donc très sensible au bruit, qui nuit gravement à la qualité de l'approximation des contours.

Dans la plupart des techniques proposées, plusieurs opérateurs locaux de dérivation du premier ordre et du second ordre sont utilisés suivis respectivement par une recherche des maxima locaux et de passages par zéro [BALL82]. Ces opérateurs effectuent le filtrage et la dérivation de l'image localement, d'où leur nom de filtre à réponse impulsionnelle finie (FIR). Les plus connus sont les filtres de Prewitt et de Sobel.

Depuis quelques années, une nouvelle approche est proposée, basée sur des filtres à réponse impulsionnelle infinie (IIR). L'approche de Canny [CANN86] est basée sur un opérateur optimal en fonction d'un critère basé sur la détection et la localisation. Les travaux de Deriche [DERI87] [DER'87] et Shen et Castan [SHEN91] ont repris cette démarche et proposé des opérateur plus simples et présentant de meilleurs indices de performance.

Pour obtenir à partir d'images souvent bruitées, des contours correspondant aux caractéristiques énoncées dans le paragraphe précédent, les algorithmes comprennent plusieurs étapes qui peuvent être confondues lors de l'implémentation des algorithmes:

- Filtrage passe-bas afin d'atténuer l'influence du bruit dans les images.

- Détection de contours: extraction d'un ensemble de points présentant les caractéristiques d'un contour.

- Localisation des contours: à partir de l'ensemble précédent, détermination de la position du contour et élimination des faux contours.

- Chaînage des points contours.

L'étape de chaînage consiste à relier les points contours connexes obtenus à l'étape précédente, soit à partir des maxima locaux dans la méthode de Deriche, soit les passages par zéro du Laplacien pour Shen et Castan.

Dans la méthode de Shen et Castan, ces contours sont formés et chaînés au fur et à mesure du choix des meilleurs chemins dans le graphe.

Le chaînage est suivi d'un codage du contour soit point par point, soit par des polygones, voire des arcs ou courbes paramétrées.

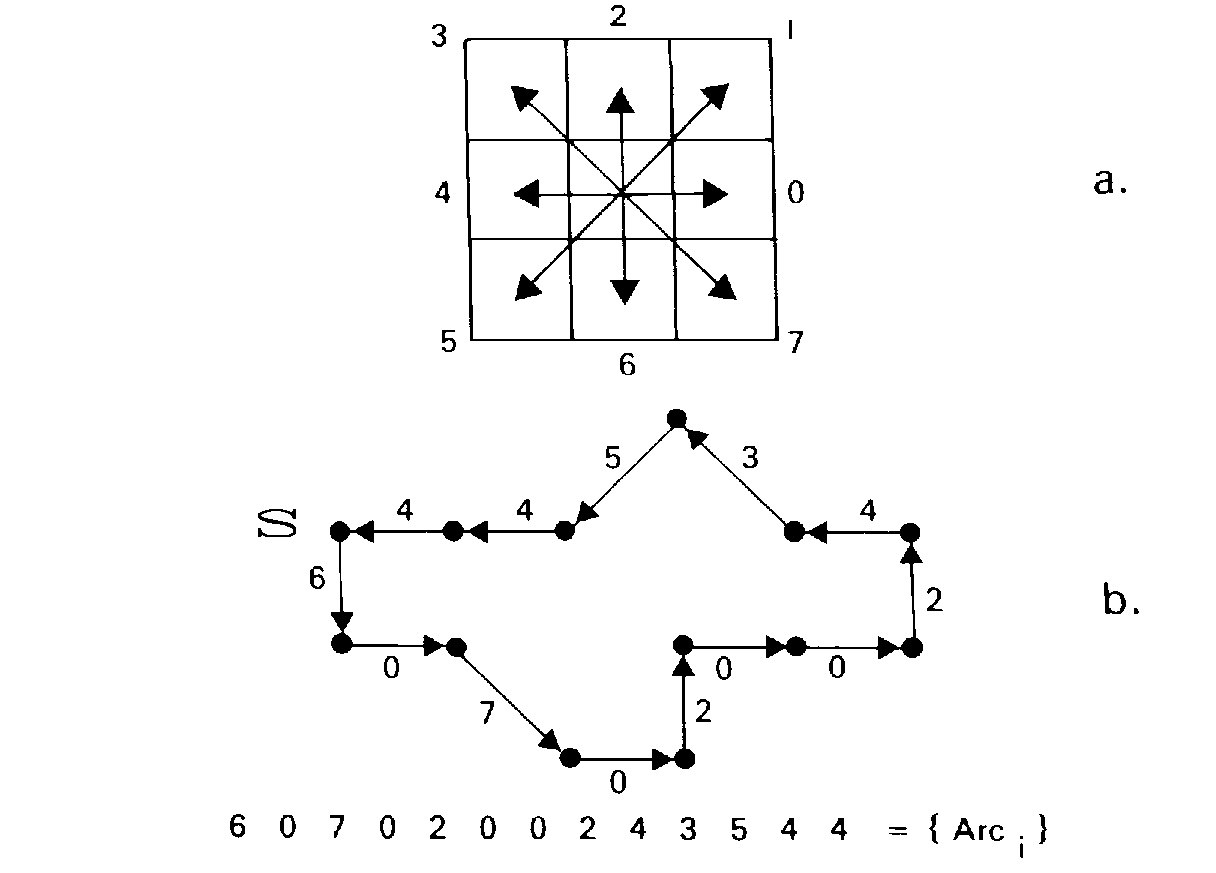
Le codage que nous avons choisi est celui de Freeman [FREEMA] qui va nous donner par son alphabet un critère de similarité nous permettant de mettre en correspondance les contours de deux images stéréoscopiques. Son principe est de décrire les arcs formant un contour par une suite de vecteurs de taille élémentaire et de direction choisie dans un ensemble fini. La direction d'un arc est codée par une valeur comprise entre 0 et 7 dans le sens trigonométrique comme le montre la figure suivante.

L'écart entre deux valeurs du codage de Freeman représente 45° ce qui est assez imprécis, et la longueur des segments correspondant aux directions (0,2,4,6) est de un pixel alors que la longueur des segments de direction (1,3,5,7) est de 1.414 pixels ce qui entraîne une variation du nombre d'éléments codant une longueur donnée suivant l'orientation du segment de contour. Cependant, dans le cas d'une mise en correspondance, ces désavantages peuvent être atténués si l'on choisit des points de correspondance dans les zones de changement de direction. Cette méthode est de toute façon moins critique que la mise en correspondance de courbes ou de segments de droites pour lesquels l'approximation exacte nécessite une extraction et une segmentation optimales des contours sur les deux images homologues.

Le problème de la rotation d'une image par rapport à l'autre peut être résolu en utilisant un codage relatif des arcs du contour comme le montre la figure suivante qui présente le codage absolu et relatif d'un même contour.

Dans cet exemple chaque direction est codée par rapport à la direction précédente. Cette méthode est trop localisée et affaiblit le codage en tant que critère de similarité entre deux contours. En effet, la direction entre deux arcs successifs variera en général d'une unité de direction à cause du lissage des contours par les algorithmes utilisées. Nous avons donc choisi le codage d'un arc i par rapport à l'arc i-k en choisissant k entre 5 et 20 pour bénéficier à la fois de l'ensemble des valeurs de codage possibles et du codage relatif d'un arc. Pour un arc i, i=1..nombre d'arcs, la fonction de codage relatif R à partir des valeurs absolues A est:

Ainsi la chaine codée en absolu: (0,7,0,1,0,6,5,4,6,3,2) est codée (0,7,1,1,7,6,7,7,2,5,7) pour k=1 et (0,7,1,1,7,6,6,4,5,3,4) pour k=5.

Les résultats présentés dans le chapitre suivant montrent que notre choix constitue un bon compromis qui permet une bonne caractérisation des couples de points homologues, confirmée par la qualité de la mise en correspondance des images.

Nous avons testé les méthodes de Deriche et de Shen et Castan sur trois types d'images: images de caméra, images optiques de photographie aérienne et images de microscopie électronique.

Le résultat des traitements effectués est présenté ci-dessous, les contours sont ensuite codés sur l'alphabet de Freeman en relatif en choisissant un sens de codage orienté par rapport au gradient.

Nous avons extrait les contours des images test selon les méthodes de Deriche d'une part, et de Shen et Castan d'autre part. Les résultats obtenus sont similaires avec une exécution plus rapide pour la méthode de Shen et Castan. Un affinage des seuils permettrait d'améliorer la qualité des contours obtenus, cependant les résultats sont suffisant pour les étapes suivantes de la chaîne de traitement.

Dans le travail présenté, l'extraction de contour est surtout un moyen d'obtenir des points homologues entre deux images stéréoscopiques afin de préparer les étapes de calibration du système de prise de vues et de mise en correspondance des deux images. Il n'est donc pas nécessaire d'obtenir le maximum de contours sur une image mais plutôt d'extraire les contours les plus fiables possibles. Un nombre trop élevé de contours serait un désavantage par l'explosion combinatoire de la recherche de correspondance entre contours homologues.

D'autre part, les modèles utilisés pour rehausser les contours ne sont pas forcément optimaux pour des images de microscopie électronique, puisque les contours qui présentent un pic lumineux importants, n'ont pas exactement les mêmes propriétés que ceux d'images optiques, et les propriétés statistiques du bruit ne sont pas les mêmes que pour les images optiques (bruit blanc).

Nous avons donc testé ces deux détecteurs de contours sans les affiner puisque le plus important était d'obtenir une chaîne de traitement complète. Il sera intéressant de tester l'enchaînement de différents filtrages (Sobel, Deriche ou Shen & Castan) avec les méthodes de sélection de points ( max local, Laplacien ou programmation dynamique) afin de déterminer pour chaque type d'image la solution la mieux adaptée.

Suite