
3. Géométrie
Ce chapitre est dédié à une étude de la géométrie d'un système de stéréovision et des solutions que nous proposons.
Notre méthode nous permet de travailler en trois étapes:
1) en deux dimensions afin de calculer les épipoles dans les plans images. Ces points nous aideront à traiter le problème dans l'espace et à mettre les deux images en correspondance.
2) dans un espace projectif afin de calculer les coordonnées projectives des points appariés sans connaissance préalable de la position des points de référence dans l'espace.
3) en trois dimensions par simple passage de l'espace projectif à l'espace cartésien, grâce à la matrice de changement de repère calculée à partir des coordonnées cartésiennes des points de référence.
Nous présentons les notions nécessaires à la compréhension de notre méthode, puis le problème et la solution proposée dans le cas de projection centrale et parallèle. Enfin, nous abordons l'expérimentation de notre méthode sur des ensembles de points générés artificiellement pour valider notre solution.
Les applications de ce travail se trouveront dans le chapitre 5 de mise en correspondance pour la partie bidimensionnelle et dans le chapitre 6 de calcul 3D pour les aspects tridimensionnels.
3.1 Coordonnées homogènes
Rapportons l'espace de dimension n à un repère cartésien. A tout élément non nul de Rn+1 noté (X,Y,Z,T) pour n=3, nous pouvons associer :
- si T<>0 le point M de coordonnées cartésiennes (x=X/T, y=Y/T, z=Z/T)
- si T=0 le "point à l'infini" (convention de langage) M dans la direction que définit dans l'espace ordinaire le vecteur non nul (X,Y,Z).
Dans les deux situations, deux points M et M' coincident si et seulement si (X,Y,Z,T) et (X',Y',Z',T') sont proportionnels.
Inversement, à tout point donné (au sens ordinaire ou "à l'infini"), correspond une infinité de systèmes (X,Y,Z,T) possibles (et non nuls) proportionnels. L'un d'entre eux est généralement retenu sous le nom de coordonnées homogènes du point M.
Ainsi (0,0,0,1) représente l'origine des axes, (1,0,0,0), (0,1,0,0) et (0,0,1,0) leurs points à l'infini (directions), et le système (1,1,1,1) représente le point unitaire qui sert à déterminer la graduation des axes. L'ensemble de ces n+2 points est un repère projectif que nous notons Ro.
Si nous considérons les points Mi (Xi,Yi,Zi,Ti) avec 0<i<n+2,
pour n=3: quatre points Mi sont dans un même plan si et seulement si :
|
|X1
X2 X3 X4 | |
pour n=2: trois points Mi sont alignés si et seulement si :
| X1 X2 X3 |
|
Y1 Y2 Y3 |
= 0
| T1 T2 T3 |
pour n=1: deux points Mi sont confondus si et seulement si :
|
X1 X2 |
|
T1 T2 |
= 0
La souplesse des coordonnées homogènes se manifeste donc surtout dans les problèmes projectifs où n'interviennent que des points, droites, plans à identifier, droites concourantes, plans ayant une droite commune, notions qui se ramènent à une dépendance linéaire dans un espace vectoriel, entre éléments non nuls.
3.2 Coordonnées projectives
On appellera plus généralement repère projectif R tout système de n+2 points Mi tels que (n+1) quelconques d'entre eux soient indépendants (c'est à dire non coplanaire si n=3, non alignés si n=2, non confondus si n=1). Le (n+2)ème point joue le rôle de point unitaire, ce qui signifie en prenant n=2 qu'il existe des coefficients non nuls p1, p2, p3,p4 tels que:
|
|p4.X4| |p1.X1| |p2.X2|
|p3.X3| |X1 X2 X3| |p1| |p4.X4| |
Ces coefficients sont définis à un facteur de proportionnalité près, on est donc resté fidèle au principe des coordonnées homogènes. Cependant, pour des raisons de commodité, on choisit généralement p1=p2=p3=p4=1.
En pratique, ces quatre points étant "à distance finie", on simplifie en prenant M4 au centre de gravité du triangle M1,M2,M3, ce qui revient à choisir T1=T2=T3=p1=p2=p3=1,T4=3 et p4=1.
Changement de coordonnées: Le passage de Ro (du paragraphe précédent) à R permet de représenter un point M par un nouveau système de coordonnées. si on les note (X',Y',T'), la formule de passage est:
|
-1 |
comme en algèbre linéaire. Mais il faut remarquer que les coordonnées
(X,Y,T) et (X',Y',T') sont des coordonnées homogènes.
Un tel système (X',Y',T') est un système de coordonnées projectives dans le repère R.
L'emploi de ces coordonnées reste techniquement le même. Ainsi l'équation d'une droite est toujours de la forme uX + vY + wT = 0. Celle qui joint les points de coordonnées (a,b,c) et (a',b',c') dans R est:
|X a a'|
|Y b b'|
= 0
|Z c
c'|
Les sommets M1(1,0,0), M2(0,1,0), M3(0,0,1) et le point unitaire M4(1,1,1) du repère R sont respectivement associés à M1(X1,Y1,T1), M2(X2,Y2,T2), M3(X3,Y3,T3) et M4(X4,Y4,T4). Tout se passe comme dans Ro du point de vue calcul, même si (0,0,1) est cité ici en troisième position à cause des habitudes matricielles.
3.3 Les homographies
3.3.1 Dimension 1
Considérons deux droites D et D' munies chacune d'un repère projectif R et R' respectivement.
Une homographie H: D -> D' est une application bijective définie par une matrice inversible:
H =|a b|
|c d|
de sorte que M(X,T) ait pour image M'(X',T') telle que (X',T')=H(X,T).
Propriétés:
1) La transformation ne change pas en remplaçant H par une matrice proportionnelle.
2) Si un changement de repère projectif est effectué de matrice P pour R, P' pour R', on substitue simplement à (X,T) et (X',T'): P(X,T) et P'-1(X',T'). Donc H est remplacée par: H'= P'-1.H.P qui est toujours une matrice inversible. La notion d'homographie H a donc un caractère intrinsèque.
3) Si on compose H avec une homographie H': D' -> D" (avec repère R"), H o H' est encore une homographie (de matrice H'H dans les repères R,R").
4) H-1: D' -> D est une homographie.
5) Dans le cas où D'=D on pourra donc parler du groupe des homographies de la droite D.
Notion de birapport:
Ce paragraphe a un rôle purement descriptif puisque dans notre méthode, nous n'utilisons pas les birapports.
Prenons R=Ro et R'=Ro' pour retrouver les coordonnées cartésiennes usuelles sur D et D', x=X/T et x'=X'/T' donnent x'=(ax+b)/(cx+d). C'est la fonction homographique classique (ad-bc<>0) complétée par :
- "l'infini" a pour image le point (a,c), généralement à distance finie sur D'.
- le point (-d,c) de D généralement à distance finie sur D a son image "à l'infini" sur D'.
Appelons M1', M2', M3' et M4' les images de quatre points M1, M2, M3, M4. On a:
(x' - x1') / (c' - x2) = k. (x - x1)/(x - x2) où k = (c.x2 + d)/(c.x1 + d)
donc:
x3' - x1' x4' - x1' x3 - x1 x4 - x1
--------- : --------- = ------- : -------
x3' - x2' x4' - x2' x3 - x2 x4 - x2
Ce nombre est dit birapport des quatre points énumérés dans cet ordre et noté (M1,M2,M3,M4). L'homographie a conservé le birapport. Inversement, une transformation ponctuelle de D dans D' conservant le birapport sera de la forme :
|
|
La notion de birapport est donc fondamentale en géométrie projective. Elle sert même à caractériser les homographies en dimension 1. C'est l'invariant projectif fondamental.

Figure 3.1 Birapport de quatre points sur deux droites
Remarque:
si R est défini par (M1,M2,M3) et R' par (M1',M2',M3'), alors l'homographie est définie par une matrice:
|a 0|
|0 a|
qui se ramène à l'identité, c'est à dire que des points homologues par H auront les mêmes coordonnées projectives respectivement dans R et dans R'. Une telle simplification est parfois très utile.
3.3.2 Dimension 2
On considère deux plans P et P' munis chacun d'un repère projectif R et R' respectivement.
Une homographie H: P -> P' est une application bijective définie par une matrice inversible 3x3: H telle que l'image de M(X,Y,T) soit M':(X',Y',T') = H (X,Y,T).
Propriétés:
Les cinq propriétés citées en dimension 1 sont toujours valables.
L'image d'une droite D appartenant à P est une droite D'.
La restriction de H à D et D' est une homographie: D -> D', ce qui entraîne que l'homographie H conserve aussi les birapports de quatre points alignés. Ceci trouve son application dans le birapport de quatre droites coplanaires concourantes D1,D2,D3,D4. Si deux droites D et D' les coupent respectivement en M1,M2,M3,M4 et M1',M2',M3',M4' alors (M1,M2,M3,M4) = (M1',M2',M3',M4'). Ce nombre est appelé birapport de ces quatre droites et noté (D1,D2,D3,D4).
3.3.3 Dimension 3
Les propriétés des dimensions 1 et 2 sont toujours valables.
L'espace permet de voir dans une homographie de plan à plan H: P -> P' qui envoie Mi sur Mi' (i=1,2,3,4) (formant respectivement des repères projectifs de P et P') la restriction d'une homographie de l'espace en lui même.
Le cas particulier où les droites (Mi,Mi') se coupent en un point S constitue une perspective ou une projection de P sur P' à partir de S. Les perspectives conservent donc aussi les birapports. Si L est l'intersection des plans P et P', deux droites D et D' de P et P' se coupent en L, et pour quatre couples, on met en évidence la conservation du birapport des quatre droites concourantes coplanaires par homographie.
3.4 Problème de la stéréoscopie
Définition:
Etant donné un objet de l'espace, on appelle image d'un point P sur un plan donné Q à partir d'un centre (optique) C le point d'intersection M de Q avec la droite (C,P).
Problème:
On suppose connues deux images planes d'un assez grand nombre de points de l'objet Pi sur deux plans Q et Q' à partir de deux centres C et C': images Mi et Mi' supposées identifiées.
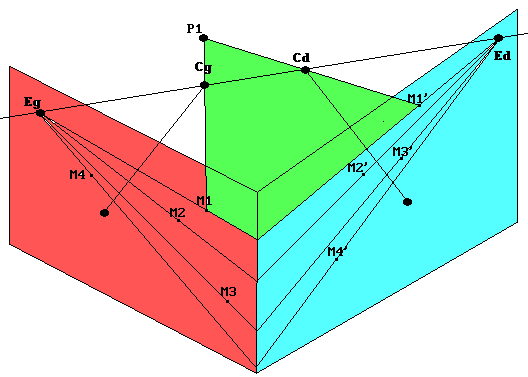
Fig. 3.2: Schéma de base de la géométrie épipolaire
On ne peut reconstituer l'objet à partir de ces seules images, mais si l'on dispose à l'avance de cinq points identifiés P1,P2,P3,P4,P5 (tels que quatre d'entre eux ne soient jamais coplanaires) de cet objet, montrons que la reconstitution est possible.
Pour résoudre ce problème nous présentons un cas particulier et une méthode pour nous ramener du cas général à ce cas particulier.
3.4.1 Cas particulier
Considérons le cas particulier où les deux plans images Q et Q' coincident avec un plan q défini par P1, P2 et P3 connus. Appelons m et m' les deux images d'un point P inconnu sur q à partir de C et C', et e point épipolaire l'intersection de la droite (C,C') avec q.

Figure 3.3: Cas particulier de stéréovision
m et m' sont alignés nécessairement avec e qui est donc identifiable si l'on dispose d'au moins deux couples de points.
Si nous connaissons P4, m4 et m4', nous disposons par là même du plan (e,C,C',P4). Il suffit donc de connaître aussi P5, m5 et m5' pour déterminer:
- La droite (C,C') comme intersection des deux plans (e,C,C',P4) et (e,C,C',P5).
- Le point e comme intersection des deux droite coplanaires (m4,m4') et (m5,m5').
- Le point C dans l'espace comme intersection des droites (P4,C,m4) et (P5,C,m5).
- Le point C' dans l'espace comme intersection des droites (P4,C,m4') et (P5,C,m5').
Par suite tout autre couple d'images mi et mi' définira le point Pi dans l'espace comme l'intersection des droites (C,mi) et (C',mi').
3.4.2 Cas général
Dans la pratique, nous n'avons pas la possibilité de savoir comment étaient disposés au départ les plans Q et Q' dans l'espace.
Appelons E et E' les points épipolaires qui correspondent à l'intersection de la droite (C,C') respectivement avec les plans Q et Q'.
Conservons le plan q présenté dans le cas particulier et défini par les points P1,P2 et P3. L'alignement de E,E' et e nous invite à envisager une méthode projective pour résoudre le problème. La figure suivante présente la situation des trois plans Q, Q' et q dans l'espace.

Figure 3.4 : relation entre les plans Q, Q' et q dans l'espace
Remarque: Tous les points présenté sur cette figure sont coplanaires.
Notations:
Dans la suite de notre présentation nous utiliserons les notations suivantes:
les images d'un point sur un plan image seront notées en majuscules, et les images du même point sur le plan q seront en minuscules. Un point P aura donc pour projection M sur Q par C, M' sur Q' par C', m sur q par C et m' sur q par C'.
Principe de la méthode de calcul:
Considérons un plan q de l'espace supposé connu, nous projetons le plan Q sur q par le centre optique C, et le plan Q' sur q par le centre optique C'. Les projections de Q sur q et Q' sur q sont des homographies de plan à plan:
H1: Q -> q et H2: Q' -> q.
Si nous reprojetons l'image du plan Q' sur q vers le plan Q par le centre C, nous appliquons l'inverse de H1 sur H2(Q').
Le paragraphe précédent nous a présenté les propriétés des homographies. L'inverse d'une homographie étant une homographie et la composition de deux homographies étant aussi une homographie, il en résulte que cette double projection Q' -> q -> Q est aussi une homographie H.
Celle ci pour être calculée nécessite la connaissance de quatre points coplanaires homologues sur les deux images. Cependant, la géométrie épipolaire nous donne l'alignement des points homologues dans q avec e qui est l'intersection de la droite (C,C') avec le plan q. Nous choisissons trois couples de points homologues (P1,P2,P3) (P1',P2',P3') plus un point unitaire pris arbitrairement, comme base projective sur les deux images. Après passage en coordonnées projectives des deux ensembles de points homologues (Pi, Pi'), nous calculons une homographie H entre Q et Q' qui superpose les points de la base projective P1=H(P1'), P2=H(P2'), P3=H(P3'), et aligne tous les couples Pi, H(Pi') avec un point E qui correspond à l'épipôle sur le plan Q.
Cette méthode nécessite la connaissance d'un ensemble de 8 points appariés entre les deux images.
Ensuite, il est possible de recalculer les points Mi' de l'image homologue dans l'image de référence par la relation Mi"=H(Mi'). Si nous connaissons l'homographie H entre Q et Q', et cinq points (P1,P2,P3,P4,P5) dans l'espace ainsi que leurs traces (M1,M2,M3,M4,M5) sur Q et (M1',M2',M3',M4',M5') sur Q', nous calculons H(M1',M2',M3',M4',M5') = (M1",M2",M3",M4",M5") dans Q.
Pour nous ramener au cas particulier présenté en début de sous chapitre, il reste à calculer l'homographie H1 entre Q et q ainsi que la position de C et C' soit 6 coordonnées et les deux coefficients de H1.
Ils peuvent être calculés grâce à la connaissance de P4,P4' et P5,P5' par les alignements:
(C,P4,m4), (C',P4,m4'), (C,P5,m5), et (C',P5,m5')
avec m4=H1(M4), m4'=H1(M4"), m5=H1(M5) et m5'=H1(M5"),
ce qui fournit un système linéaire de huit équations et huit inconnues.
Il est possible de calculer C et C' dans l'espace projectif, en prenant P1,P2,P3,P4,P5 comme base projective dans l'espace avec P5 comme point unitaire. Les coordonnées sont alors fixées arbitrairement et permettent de calculer C et C' dans cette base. Le passage à l'espace cartésien se fait par un simple changement de base.
Démonstration:
Introduisons M" en projetant m' sur Q à partir de C, et montrons que l'application H: Q' -> Q , M' -> M" est une homographie et qu'il est possible de la préciser.
C'est en effet une composée d'homographies:
- de Q vers q: M' -> m' induite par la perspective de centre C'
- de q vers Q':m' -> M" induite par la perspective de centre C
H transforme les points M1',M2',M3',E' dans Q' en M1",M2",M3",E dans Q par l'intermédiaire de P1,P2,P3,e dans q. D'autre part, toutes les droites (M,M") de Q concourent en E.

Figure 3.5 : relation entre les points dans le plan (C,C',P)
a) Relations entre les plans images
Rapportons Q au repère projectif R formé par M1,M2,M3 et comme point unitaire le centre de gravité de M1,M2,M3. Aux coordonnées cartésiennes (xi,yi) d'un point Mi de Q, on associera le système de coordonnées projectives (Xi,Yi,Zi) défini par:
|
-1
|
Formule de passage en coordonnées projectives
on sait que l'on peut multiplier Xi,Yi,Zi par un nombre différent de zéro arbitraire, ce nouveau système détermine le même M, il n'y a bien que deux paramètres effectifs par point.
Rapportons Q' à un repère R' à partir de M1', M2', M3' de façon analogue. L'homographie transformant un point M' de R' en M" dans R sera définie par une matrice diagonale car à (1,0,0) dans R, correspond (1,0,0) dans R' (idem pour (0,1,0) et (0,0,1)). Les formules:
| |
Xi" |
|
a 0 0 |
|
Xi' |
| Yi" | = | 0 b 0 | | Yi' | | Zi" | | 0 0 c | | Zi' | |
A noter que les nombres a, b et c sont définis à un facteur de proportionnalité près et qu'ils sont encore inconnus, de même que la position de E.
Soit (Ex,Ey,Ez) un système de coordonnées projectives de E dans R. Utilisons le fait que les droites Di(Mi,Mi") se rencontrent en E, c'est à dire:
| | Ex Xi a.Xi' | | Ey Yi b.Yi' | = 0 | Ez Zi c.Zi' | |
Equ.1: Système d'équations de l'alignement (E,Mi,H.Mi')
ce qui n'a d'intérêt que pour les indices i>3 puisque les points d'indice 1,2,3 ont les mêmes coordonnées projectives. Prenons trois tels indices i,j,k distincts. La compatibilité en Ex, Ey et Ez des trois équations entraîne:
|c.Yi.Zi'-b.Yi'.Zi a.Zi.Xi'-c.Zi'.Xi b.Xi.Yi'-a.Xi'Yi| |c.Yj.Zj'-b.Yj'.Zj a.Zj.Xj'-c.Zj'.Xj b.Xj.Yj'-a.Xj'Yj| = 0 |c.Yk.Zk'-b.Yk'.Zk a.Zk.Xk'-c.Zk'.Xk b.Xk.Yk'-a.Xk'Yk| |
Equ.2: Système d'équations des coefficients de l'homographie
que l'on peut ramener compte tenu de son homogénéité à la forme:
| A.b/c + A'.c/b + B.c/a + B'.a/c + C.a/b + C'.b/a + D = 0 |
deux telles équations de ce type (avec deux triplets i,j,k différents) suffisent à priori, puisqu'il n'y a que deux inconnues véritables (par exemple a/c et b/c), mais puisqu'on dispose d'un nombre suffisant de couples de points Mi,Mi', il est préférable de les traiter comme équations linéaires de la forme A.x1 + A'.x2 + B.x3 + B'.x4 + C.x5 + C'.x6 + D = 0 à six inconnues x1, x2, ..., x6.
Pour cela nous avons besoins d'au moins 5 points qui pris trois à trois nous fournissent 10 équations nous permettant de résoudre le système au moindres carrés. Au total, cette méthode nécessite 3 points de base + 5 points secondaires pour résoudre le système, soit 8 points homologues connus sur les deux images.
Après coup, on vérifiera qu'il est possible de contrôler la validité des points choisis puisque x1.x2 = x3.x4 = x5.x6 = 1.
L'homographie H étant ainsi déterminée, le point E sera à son tour déterminé par le système linéaire d'équation d'alignement (E,Mi,H.Mi'), puis de même E' = H-1(E).
b) Relations dans l'espace
Revenons maintenant à l'espace, prenons le repère projectif R* formé par P1, P2, P3, P4 et pour point unitaire le centre de gravité de ces quatre points, pour conserver la même technique de passage cartésienne - projective. Il est possible de choisir P5 comme point unitaire mais sans aucun intérêt technique, sinon de pouvoir calculer la position des points dans l'espace projectif, le point P5 intervenant alors dans le passage en coordonnées cartésiennes.
En restriction au plan q, celui-ci se trouve muni du repère r* (P1,P2,P3 et comme point unitaire le centre de gravité de ces trois points).
On a envisagé plus haut l'homographie q -> Q, m -> M, m' -> M" induite par la perspective de centre C.
Si les coordonnées projectives de m dans r* sont notées (x*, y*, z*), celles de M associé seront de la forme:
|
| X | |
u 0 0 | | x* |
| Y | = | 0 v 0 | | y* | | Z | | 0 0 w | | z* | |
Matrice diagonale de l'homographie u,v,w
où la matrice diagonale définit l'homographie (u.v.w<>0).
Elle est diagonale puisque P1 -> M1, P2 -> M2 et P3 -> M3.
On aura donc m: (X/u, Y/v, Z/w) et m':(X"/u, Y"/v, Z"/w) avec X"=a.X', Y"=b.Y' et Z"=c.Z'.
Montrons que l'on peut préciser aussi cette homographie grâce à la connaissance de P4 et de P5.
On se sert du fait que (1) (P4,m4) et (P5,m5) se coupent en C dans le plan (P4, P5, m4, m5), et de même (2) (P4,m4') et (P5,m5') se coupent en C' dans le plan (P4, P5, m4', m5').
Les coordonnées projectives de P5 dans le repère spatial étant supposées connues et notées (X5*,Y5*,Z5*,1), comme l'équation d'un plan passant par P4:(0,0,0,1) est de la forme A.x* + B.y* + C.z* = 0, on a:
(1) |X4/u X5/u X5*|
|X4 X5 u.X5*|
|Y4/v Y5/v Y5*|= 0 <=> |Y4 Y5 v.Y5*|= 0
|Z4/w Z5/w Z5*| |Z4
Z5 w.Z5*|
soit:
| (1) |X4
X5 u.X5*|
(2) |X4"
X5" u.X5*|
|Y4 Y5 v.Y5*| = 0 et |Y4" Y5" v.Y5*| = 0 |Z4 Z5 w.Z5*| |Z4" Z5" w.Z5*| |
Equ.3: Système d'équations de l'homographie u,v,w
Ces deux équations (A.u + B.v + C.w = 0 et A'.u + B'.v + C'.w = 0) définissent u,v et w à un facteur de proportionnalité près. L'homographie est donc déterminée: u=BC'-CB', v=CA'-AC', w=AB'-BA' ou des nombres proportionnels.
Notons que e l'est aussi, comme intersection des droites (m4,m4') et (m5,m5'), ou comme transformée par l'homographie de E qui est connu.
Détermination de C:
Les coordonnées projectives dans R* de m4 sont (X4/u,Y4/v,Z4/w,0), donc celles de C aligné avec P4: (0,0,0,1) et m4 sont de la forme (s.X4/u, s.Y4/v, s.Z4/w, 1), s étant inconnu.
C étant aligné avec P5 et m5, on une dépendance linéaire de (s.X4/u, s.Y4/v, s.Z4/w, 1), (X5*,Y5*,Z5*,1) et (X5/u,Y5/v,Z5/w,0).
On a donc par exemple à l'aide des deux premières coordonnées:
| s
= X5*.u.Y5 - Y5*.v.X5 ------------------- X4.Y5 - X5.Y4 |
Dépendance linéaire entre C et les projections de M4 et M5
On détermine C' de la même façon.
Nous sommes maintenant ramenés au cas particulier vu au début, le problème est résolu.
3.4.3 Cas de la projection parallèle
Dans ce cas particulier de la projection parallèle, les points C et C' sont rejetés à l'infini dans deux directions D et D' a priori inconnues.
Les calculs pourront donc ici légitimement privilégier les points à distance finie.
Cette fois la reconstruction est possible avec la connaissance de quatre points seulement que nous appelons P1, P2, P3 , P4 et qui forment un vrai tétraèdre. Aucune des homographies envisagées dans le cas général ne nécessite de calculs. L'application m -> M de q dans Q induite par projection parallèle est une affinité, conserve les barycentres (comme tous les rapports au sens de Thalès).
m a donc dans P1,P2,P3 mêmes coordonnées barycentriques que M dans M1,M2,M3.
m' a de même dans P1,P2,P3 les coordonnées barycentriques de M' dans M1',M2',M3'.
Si on connaît M4, M4' et P4, on en déduit m4 et m4', les droites (m4,P4) et (m4',P4) ont les directions D et D' que l'on recherche.
A tout autre couple Mi,Mi' on associera de même mi,mi' par lesquels il suffira de mener les parallèles à D et D' pour obtenir le point objet Pi.
A noter que tous les segments m,m' sont parallèles, l'épipôle e de la théorie est en effet à l'infini dans P1,P2,P3 et l'alignement C,C',e se fait à l'infini.
Rappel:
Les coordonnées barycentriques pour un point M par rapport à M1, M2 et M3 sont les trois nombres X, Y, Z tels que :
|
-->
--> --> -> |
Définition de coordonnées barycentriques
A noter que (X,Y,Z) interviennent de manière homogène (coefficients barycentriques), la technique "projective" est encore visible ici.
Elles s'obtiennent donc comme nous l'avons déjà vu par :
| |
x |
|
x1 x2 x3 |
|
X |
| y | = | y1 y2 y3 | | Y | | 1 | | 1 1 1 | | Z | |
Passage en coordonnées barycentriques
3.4.4 Moindres carrés
Si l'on dispose d'un nombre suffisant de points appariés, on peut améliorer l'évaluation de l'homographie entre les plans images et la position des points E et E' par la méthode des moindre carrés lors de la résolution des système linéaires.
Tout modèle linéaire peut être représenté sous la forme :
| y
= X . beta + epsilon (n,1) (n,p) (p,1) (n,1) |
où y est le vecteur des observations
X est une matrice connue fixée
beta est le vecteur des paramètres à estimer
epsilon est le vecteur "erreur" distribué en alpha(0,s2 )
n est le nombre d'observations
p est le nombre de paramètres à évaluer (n>p)
Théorème de Gauss-Markov:
Le meilleur (de variance minimum) estimateur non biaisé de beta est l'estimateur des "moindre carrés".
beta* = (X'.X)-1 X
avec l'espérance
E(beta*) = beta
et la variance
var(beta*) = s2 (X'X)-1
3.5 Expérimentation
3.5.1 Relation entre plans images
Nous avons testé la méthode sur le modèle théorique présenté ci-dessous. Les points ont été choisis arbitrairement sur une figure avec pour seule propriété le fait que les points "homologues" sont sur des lignes passant par les deux centres des faisceaux et dont les intersections deux à deux se trouvent sur une même droite.
Les deux faisceaux de droites de la figure présentent une relation homographique et nous cherchons à calculer les centres épipolaires gauche et droit. Les coordonnées des points gauches et droits sont définies par rapport à deux repères distincts pour les deux zones de l'image.

Fig.3.6: Ensemble de points d'origine sur les plans P et P'
Après avoir calculé l'homographie entre les deux faisceaux de droites avec comme base projective les couples de points (1,2,3,4) et en suivant la méthode présentée précédemment, nous avons recalculé tous les points de la partie droite dans le repère gauche en trois temps:
1) Passage de coordonnées cartésiennes (xd,xd) dans le repère cartésien R2 en coordonnées projectives (Xd,Yd,Zd) dans le repère projectif R2'.
2) Transformation des coordonnées par l'homographie (a,b,c), et obtention des coordonnées (aX,bY,cZ).
3) Passage en coordonnées cartésiennes (Xg,Yg) dans le repère gauche à partir des coordonnées (aX,bY,cZ).
Les tableaux suivants présentent les étapes intermédiaires de notre calcul.
|
X1 |
Y1 |
Z1 |
X2 |
Y2 |
Z2 |
|
1.5000 |
0.0000 |
0.0000 |
-0.5000 |
-0.0000 |
0.0000 |
|
0.0000 |
-0.3000 |
0.0000 |
-0.0000 |
0.4000 |
0.0000 |
|
0.0000 |
0.0000 |
0.2727 |
0.0000 |
-0.0000 |
2.0000 |
|
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
1.5000 |
1.8000 |
1.6363 |
1.8333 |
1.6000 |
1.3333 |
|
0.0000 |
0.9000 |
1.0909 |
1.8750 |
1.9500 |
-0.2500 |
|
1.5000 |
2.7000 |
2.4545 |
2.5000 |
2.4000 |
0.0000 |
|
0.0000 |
1.5000 |
1.6363 |
1.6667 |
2.0000 |
-1.3333 |
Homographie: a=-7,3333, b=-2.75, c=1, errmc=0.0000, errcoef=0.0000
|
X1 |
Y1 |
X2 |
Y2 |
|
4.0000 |
4.0000 |
3.999999 |
4.000000 |
|
2.0000 |
6.0000 |
2.000001 |
5.999999 |
|
3.0000 |
8.0000 |
3.000000 |
7.999998 |
|
7.0000 |
12.0000 |
1.230771 |
8.153844 |
|
10.0000 |
16.0000 |
0.769233 |
8.615382 |
|
6.0000 |
14.0000 |
-0.470585 |
8.117645 |
|
13.0000 |
22.0000 |
-0.499997 |
8.499997 |
|
8.0000 |
18.0000 |
-1.999995 |
7.230767 |
|
-4.9999 |
4.0000 |
-4.999990 |
4.000000 |

Fig 3.7: Résultat sur P après transformation de points de P'
Le résultat présenté sur cette figure est la visualisation graphique des coordonnées des points dans le premier repère et les droites formées par les couples de points homologues. Le centre du faisceau est l'épipôle dans le premier repère. Ce résultat correspond bien au modèle théorique, et les erreurs entre les coefficients de l'homographie, ainsi que les erreurs d'approximation aux moindre carrés sont nulles.
Après cette vérification concluante, il est intéressant d'observer l'influence du choix des points de base des coordonnées projectives (A1, A2, A3) sur la position des points recalculés et la position du centre du faisceau de droites calculé.
Nous avons choisi six combinaisons de points:
. Quatre manuellement en prenant successivement les points (1,2,3), (2,3,4), (3,4,5) et (4,5,6) de la liste des points homologues.
.une combinaison en prenant
A1: M(x,y), M'(x,y) tel que Mx minimum
A2 Mx maximum
A3 My minimum
.une combinaison en prenant les points A1, A2, A3 formant le triangle de surface maximale.
Après application de notre méthode sur ces différentes configurations, nous observons que ces points influencent fortement les résultats en ce qui concerne la position des points recalculés, mais que les centres des faisceaux restent identiques. Ceci montre l'invariance de l'épipôle lorsque l'on change les points de base et confirme la validité de notre méthode de calcul.
|
Points 1 2 3
|
Points 2 3 4 |
|
Points 3 4 5
 |
Points 4 5 6 |
|
Points MIN/MAX X Y |
Points surface max
 |
Fig 3.8: Résultat du calcul du centre épipolaire avec différents points
3.5.2 Calcul 3D en projection centrale
Pour tester cette méthode, nous avons généré artificiellement des points dans l'espace et les avons projeté de façon perspective sur deux plans de l'espace par rapport à deux centre optiques. Les valeurs test sont les suivantes:
Centre optiques: Cg(0,0,100) Cd(200,300,200)
|
Image gauche |
Image droite |
Coordonnés 3D |
||||||
|
-346.34 |
-230.89 |
2220.67 |
1343.15 |
1000.00 |
200.00 |
345.00 |
||
|
74.36 |
71.44 |
78.47 |
66.75 |
100.00 |
2.00 |
3.00 |
||
|
2.19 |
-0.73 |
10.35 |
-1.38 |
1.00 |
2.00 |
3.00 |
||
|
26.70 |
-20.92 |
-19.76 |
1.54 |
4.00 |
33.00 |
2.00 |
||
|
7.37 |
-5.89 |
4.50 |
-2.11 |
1.00 |
9.00 |
4.00 |
||
|
25.78 |
22.83 |
33.05 |
19.96 |
33.00 |
2.00 |
4.00 |
||
|
6.43 |
3.86 |
42.12 |
-28.12 |
4.00 |
1.00 |
45.00 |
||
|
104.48 |
32.72 |
50.03 |
24.67 |
65.00 |
34.00 |
33.00 |
||
|
34.96 |
15.89 |
28.65 |
14.95 |
32.00 |
12.00 |
11.00 |
||
|
3.72 |
-0.74 |
11.50 |
-2.07 |
2.00 |
3.00 |
5.00 |
||
Tableau 3.1: Coordonnées de départ dans les plans et dans l'espace
Les résultats obtenus sont les suivants:
Homographie entre l'image homologue et l'image de référence: a= -7.45 b= 0.99
Homographie entre l'image de référence et le plan P: u=-139.35 v= -1.08
Centres optiques: Cg(-0.00,-0.00,100.00), Cd(199.99,299.99,199.99)
Calcul des points dans l'espace
|
Coordonnées réelles |
Coordonnées calculées |
ErreurMC |
Dist. |
||||
|
1000.00 |
200.00 |
345.00 |
1000.00 |
200.00 |
345.00 |
0.000000 |
0.0 |
|
100.00 |
2.00 |
3.00 |
100.00 |
2.00 |
3.00 |
0.000000 |
0.0 |
|
1.00 |
2.00 |
3.00 |
1.00 |
2.00 |
3.00 |
0.000000 |
0.0 |
|
4.00 |
33.00 |
2.00 |
4.00 |
33.00 |
2.00 |
0.000000 |
0.0 |
|
1.00 |
9.00 |
4.00 |
1.00 |
9.00 |
4.00 |
0.000000 |
0.0 |
|
33.00 |
2.00 |
4.00 |
33.00 |
2.00 |
4.00 |
0.000025 |
0.0 |
|
4.00 |
1.00 |
45.00 |
4.00 |
1.00 |
45.00 |
0.000000 |
0.0 |
|
65.00 |
34.00 |
33.00 |
65.00 |
34.00 |
33.00 |
0.000004 |
0.0 |
|
32.00 |
12.00 |
11.00 |
32.00 |
12.00 |
11.00 |
0.000002 |
0.0 |
|
2.00 |
3.00 |
5.00 |
2.00 |
3.00 |
5.00 |
0.000000 |
0.0 |
Tableau 3.2 Résultats des calculs, erreur et distance entre points réels et calculés
Nous observons que les centre optiques ont bien été calculés ainsi que les points dans l'espace. La valeur ErrMC est l'erreur aux moindres carrés issue de l'intersection des deux droites (Ig,Cg) et (Id,Cd) dans l'espace 3D. La valeur Dist est la distance entre points réels et points calculés.
Les résultats montrent un calcul exact de la position des points dans l'espace ainsi que les centre optiques du système de prise de vue, ce qui confirme la démarche théorique décrite précédemment.
3.6 Conclusion
Dans ce chapitre, nous avons présenté une étude de la géométrie de la stéréovision.
Cette étude débouche sur une méthode géométrique qui permet de déterminer la relation entre les plans images d'une part, et d'autre part de calculer les points dans l'espace. Ces résultats correspondent à d'autres recherches menées indépendamment suivant une approche algébrique [FAUG92].
Elle ressemble à la rectification des images stéréoscopiques réalisée en photogrammétrie [HURA60] [CARR71] puisque la transformation réalisée par l'homographie ainsi calculée correspond à celle réalisée par les chambres claires. Ces appareils sont des systèmes optiques permettant de voir à la fois deux objets, l'un étant transformé par réflexion dans un miroir en une image virtuelle, l'autre étant vu directement à travers le miroir précédent à face réfléchissante semi-dépolie. Dans notre méthode, nous utilisons comme centre de projection les centres optiques, et calculons la géométrie épipolaire, alors que la chambre claire utilise le centre du miroir et l'oeil de l'observateur en réalisant un redressement approximatif. On peut envisager un intérêt potentiel de notre algorithme dans le domaine de la photogrammétrie.
1) La relation entre les plans images peut être définie par une méthode linéaire grâce à la connaissance de huit couples de points homologues sur les deux images. Une surdétermination du système d'équations permet une résolution aux moindres carrés qui donne une meilleure stabilité des résultats ainsi qu'un indice de validité de ce résultat. Cette technique est particulièrement utile à la mise en correspondance des images stéréoscopiques, qui concerne le chapitre 5 de ce rapport.
2) Le calcul des points est possible dans un espace projectif sans connaissance des points dans l'espace cartésien, et le calcul des coordonnées cartésiennes en 3D nécessite la connaissance cinq points dans l'espace pour la projection centrale de quatre pour la projection parallèle. L'utilisation de notre technique est réalisée dans le chapitre 6.
Notre méthode donne des solutions exactes pour les points générés artificiellement. Son application à des images réelles suppose qu'elle soit résistante au bruit qui résulte des imprécisions d'appariement, de la déformation des plans images et dans une moindre mesure de la discrétisation des plans images. Nous aborderons l'influence du bruit sur l'exactitude des reconstructions dans le chapitre 6.
Ces aspects ouvrent des perspectives de travail à partir des modèles présentés pour éventuellement aboutir à des algorithmes de correction des plans images suivant les modèles de déformation [TOSC87] [ALIR85], soit en modifiant les équations, soit par des méthodes itératives destinées à minimiser les erreurs d'autocontrôle des coefficients de l'homographie en 2D, et les résidus pour les approximations aux moindre carrés.